先日…といっても3ヶ月以上まえですが Twitter を見てたら某モビルスーツアニメに出てくるスペースコロニーの中でボールを投げると果たしてどんな軌道になるのか…？的な話が流れていて、興味をそそられたので試しに Unity 3D の物理エンジンで再現してみました。

能書きをごちゃごちゃ書く前に、まずはインストール不要のブラウザで遊べる現物のリンクを貼ります。

スペースコロニー物理シムを開く
※ダウンロードサイズ約100MB, PCブラウザ推奨

物理エンジンの限界等もありシミュレーションといっても精度はそれなりなんですが、そのかわりTPSゲーム風仕立てになっていて走り回ったりジャンプしたり、魔法の超動力エレベーターに乗って上昇したり下降したりスペースコロニーの生活で起きるであろう力学的な違和感がどんな感じかざっくり体験できるようにしてみました。

ブラウザは Chrome と FireFox で動作確認しています。Unity WebGL 公式ドキュメントでは Safari や MS Edge も対応になってますが、このアプリは WebGL2.0 の機能を使っているため動作しない可能性が高いです。また Unity WebGL はモバイル対応がまだ不完全なため iOS 端末は動作せず、Android 端末もかなりハイスペ端末でやっとギリ動く感じです。このアプリはキー操作メインの操作系のため Windows/Mac のミドルスペック以上のデスクトップ機のブラウザで見て頂くのをお勧めします。

スペースコロニーとは

宇宙に巨大な人工の居住空間を作り都市規模の人口を移住させるというSFガジェットがスペースコロニーです。1970年代にプリンストン大学のジェラルド・オニール氏によって提唱された、自転する巨大な中空のシリンダー(円筒)に太陽光を取り入れる窓と反射パネルがあるデザインが有名で『スペースコロニー』というとこのオニール・シリンダーの事を差すことが多いようです。オニール方式の他にもいくつかスペースコロニーのアイデアはあるようですが、本記事で扱うスペースコロニーはこのオニール・シリンダータイプのものになります。

オニールタイプのスペースコロニーではシリンダー(円筒)の内側の表面に住空間を構築しますが、自転による遠心力があるためシリンダーの内側に立つとまるで足元が地球における地面であるかのように錯覚する仕掛けになっています。しかしこの疑似重力は本物の重力ではないため、例えばボールを投げると地球とは微妙に異なる軌道を描いて地面に落ちます。これをビジュアルで確認してみよう、というのが本記事とアプリの主旨です。

スペースコロニーの力学

地球で感じる本物の重力は地球と物体が万有引力で引き合うことで発生しますが、スペースコロニーに立っている場合は体と地面(シリンダー壁)の引力はほぼゼロで力学的には無重力の宇宙空間に浮んでいるのと同じです。もし障害物にぶつかったりロケットを噴射するとかいった外力が加わらないなら等速直線運動──つまり方向を変えずに真っ直ぐ一定の速度で直進するような状態になっています。

例えばシリンダーシムアプリでオッサンのキャラクターが平原にボーッと立ってる状態を考えてみましょう。

平原に立ってじっとしている場合オッサンは地面すなわちシリンダー壁に対して静止しているのであって地面のほうはシリンダーの自転速度で動いている事に注意しなければいけません。シリンダーは巨大なので毎秒数度のゆっくりした回転でも壁すなわち地面の移動速度は猛烈な速さになります。このアプリの場合、半径3kmのシリンダーが毎秒3.3度ぐらいで回転して1Gの重力を発生している設計なので計算すると地面の移動速度は毎秒172m(時速617km)ぐらいになります。

というわけでボーッと立っているオッサンの体は、力学的には時速600kmぐらいでシリンダーの回転方向にすっ飛んでいこうとしてる状態になっています(Gキーを押すとベクトルの方向と長さが確認できる)。もしシリンダーの壁がなければ宇宙空間に物体を射ち出したのと同様オッサンはそのまま接線方向にすっ飛んでいってしまいます。しかしぐるっと巨大な円弧を描いたシリンダーの壁すなわち地面があるため、真っ直ぐに進もうとしているその次の瞬間にはちょっとだけセリ上がった地面にぶつかって垂直に押し上げられる方向に速度ベクトルがほんの少し変化させられます。そのような瞬間が連続して連なっているのでオッサンの体感では連続的に地面の下へ押しつけられるような力があるように感じ(遠心力)これが疑似重力として感じられるわけです。

じっと立っている場合の疑似重力はだいたいこんなイメージですが、ややこしいのが物を投げたときです。コロニーの壁である地面(…以後断りがない限り単に『地面』と表現します)に立ってボールを投げたとします。このとき手を離れた瞬間からボールは力学的に等速直線運動に入ります───ところで、言い忘れていましたがアプリ実装もこの記事全体もそうですがシリンダー内は完全な真空と思ってください(空気の影響は完全無視)。

先に述べたとおり、地面に立ち止まっていても地面自体が猛スピードで移動してるのでボールの速度ベクトルはキャラクターから見た投射速度に自転によるおよそ600km/hの速度を合成したベクトルになります。そして地球と異なりこのボールには引力による落下は発生せず、手を離れた瞬間から等速直線運動を始めます。…となると、スペースコロニーの地面でボールを投げるといきなり猛スピードでどっかへすっ飛んでいってしまうのか？？ そんな世界でとても生活できるとは思えない！もし授業中シャーペンをうっかり落すと手から離れた瞬間から時速600kmで横に座ってる人に突き刺さる凶器になってしまう！！

…もちろんそんな事はなくシリンダーシムアプリで試してもわかるように、わりと普通にまるで地球でボールを放ったかのように放物線を描いて落ちます。というのは自分自身もボールの合成ベクトルとほぼ同じくらいの猛烈な速さで移動しているので、キャラクターから見ると自転による猛烈な速度ベクトル成分はほぼ相殺されるからです。力学的には投げ出しから地面に衝突するまで単なる等速直線運動となるため、シリンダーの外の回転しない宇宙空間から見たボールの軌道は結局シリンダーの壁の一端から出て壁の別の部分に当たるまでの直線ということになります。これを内部の自転している地面に貼り付いているキャラクターから見るとキャラクターは円弧に沿って移動していくので、結果的に地球での放物線に似た軌道を観察することになるわけです。

このように投射物の速度ベクトルが自転の速度ベクトルに比して無視できるほど小さい場合、まるで地球で生活しているかのような疑似重力環境を再現できるのがオニール・シリンダー・コロニーのアイデアの優れた点のひとつでしょう。しかしもっと高速に打ち出したり、高いところから落すなど距離が伸びてくると徐々に疑似重力のまやかしがバレて違和感が現われてくるようになります。

どのキャラクターでも[1][2][3]のキーで投射物をそれぞれボール、キューブ、ロケット弾に切り変えできますが、ロケット弾で仰角を上げて発射すると、地球であれば明かにおかしいと思われるような軌道を描いて落ちるのを観察できます。ちなみにプログラマーの色気を出してロケット弾に推力があるように見えるブラストのパーティクルを実装してしまいましたが、力学演算的にはただの高速な投射物で一切加速しません。見た目だけの雰囲気エフェクトです。安定翼もついてますが空気力はまったく無しです。

ロケット弾をあちこちに向けて発射し軌道を観察すると、コロニーの円周に沿った方位では真っ直ぐ飛んでいくのに自転軸方向(宇宙港の向きまたはその反対)に飛ばすと弾道がヨレていくのがわかります。おかしい…弾道がみな右へそれていく(CV:井上真樹夫)…もしやサイレンの魔女が…ではなくスペースコロニーの上空に行くほど自転による円周速度は減っていくので発射点の地面における円周速度は余ってしまう──つまり勢い余って自転方向に進みすぎてしまうからです。したがって円周方位であってもキャラクターから見ると真っ直ぐの軌跡に見えますが、じつは自転方向へズレていて飛距離が伸びたり縮んだりしています。

コロニーの中央方面にビル街と巨大なブリッジ──構造は平らなのに山なりの坂になっている不思議橋です──を配置してありますがエレベーターを使ってこのブリッジに登りボールが落ちていくのを観察すると、今度は反自転方向へ軌道が曲がっていくのが見えます。ブリッジの高さより下にいくほど円周速度が速くなるため打ち出したときのボールの速さでは足りなくなるからですね。諸々の都合でこのシムでは水まわりは実装できませんでしたが、仮に大きな滝があったらとしたらこんな感じの流れが見えるはずです。

ちなみに“キャラクターが自転方向に移動しているので打ち上げたボールが取りのこされて後ろに曲っていく”みたいなイメージは間違いなので注意です。走行中の電車内でボールを投げたのと同様に、ボールを投げた瞬間のキャラクター本体の速度成分も合成されるのでボールだけが取り残されたりしません。取り残されるイメージでいけば自転と反対方向にヨレていくはずですが実際は自転方向にヨレます。

ホンマかいな…？と怪しまれそうなので、もうすこし正確に図と数式を用いて説明します。

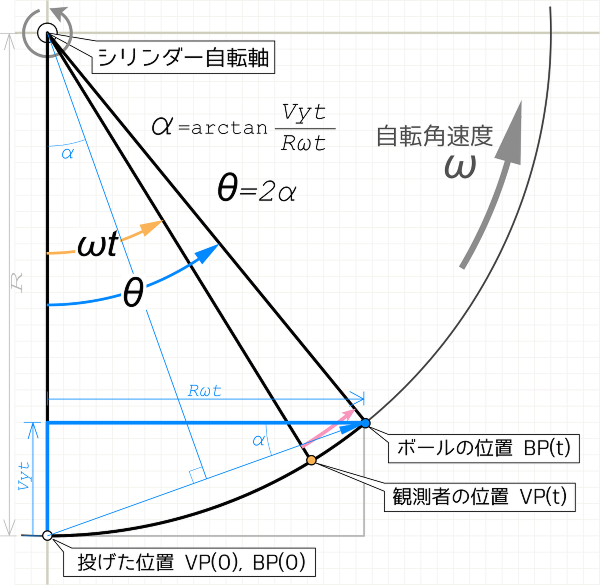
例えばボールを真上に Vy の速度で投げたとします。このとき

とします。

※厳密にはボールを投げた高さも考慮すべきですが、ややこしくなるのとシリンダー径に対し無視できるほど小さいのでここでは無視します。

図は回転しない固定宇宙空間から見たコロニー断面なので、ボールは細い水色の線の矢印の直線コースをたどって壁(地面)にぶつかります。これを自転する地面に貼り付いて移動している観測者から見上げると、真上に打ちあがったボールが自転方向にヨレながら落ちてきて地面に衝突するのが見えるはずです。自転方向にズレる事を以下に簡単な数式で説明します。

投げたポイントで手から離れた瞬間のボールのベクトルは、その瞬間の観測者 VP(0) の真上方向 Vy のベクトルに、地面の自転速度ベクトル Rω を加えた合成ベクトルです。投げた後は等速直線運動なのでそのベクトルの方向がすなわち水色のボールの軌跡と一致しているわけです。

ボールが着地点 BP(t) に到達するまでに t[sec] の時間かかったとすると、ボールの移動の水平成分は図に示すとおり Rωt になります。その t の時間の間にコロニーは ωt だけ回転し、従って観測者の位置 VP(t) の水平移動量は R sin(ωt) になります。ボールの水平移動量 Rωt より観測者の水平移動量 R sin(ωt) が小さい値になるのは明白(x > 0 のとき x > sin(x))で、ピンクの矢印で示した分だけ自転方向にボールが先行する事がわかります。

以上では真上に投げるケースについて考えてみましたが、任意の方向に投げた場合はベクトルを3軸に分解してシリンダー自転軸方向のベクトル成分(Vz)は自転の影響は無関係なので別途計算し、自転方向に平行な成分(Vx)および垂直な成分(Vy)についてのみ自転の影響を考えることになります。

そこらへんの諸々の計算式の導出はやりませんが(もうええ歳なんで正直ツラい)、図の Rωt を (Rω+Vx)t として色々コネくりまわすとイケるはずです。

 
もっと精密でより汎用的な計算式や考察はググるとちゃんとでてきますのでそちらを見ましょう。

まるで巨大な“びっくりハウス”

モノを投げたときの他にもスペースコロニーの生活では奇妙な物理現象が色々起きます。『奇妙な』といってもどれもニュートン力学で説明可能な理にかなった現象ばかりなのですが、遠心力による疑似重力がけっこう本物の重力っぽいが故になんだか奇妙な事が起こってるように感じてしまうわけです。

例えば円周に沿って自転方向に走ると重力が増え逆方向だと重力が減ります。自転による円周速度に速度を加えたり減らしたりすると遠心力が変化するので、みかけの重力も増減するわけですね。シリンダーシムアプリの SciFi ROBO でホバー(スペースキー)しながら反自転方向に加速してみましょう。SciFi ROBO は人間タイプのキャラと異なり空中でも加速するのでホバーしながら加速していくと疑似重力が減少してホバーで空中に浮きつづける状態になります。[G] キーのベロシティ表示を確認しながら完全に自転を相殺するまで加速するとホバーしなくても無重力の空間に浮ぶ状態になります。スペースコロニーに空港を建設するとしたら滑走路は円周に沿って二本平行に設置し反自転方位に離陸、着陸は自転方位で運用すると良いかもしれません。

エレベーターを使って上昇したり下降したりすると、キャラクターがズルズルと円周方向へ滑って横の力を感じます。これは自転による円周速度がシリンダーの軸に近く(つまり地面からみて上空)にいくほど小さくなるからです。キャラクターはエレベーターによって強引に垂直上昇させられるので、余った速度を減速する力が必要になるわけです(もし力を加えなければ自転方向へ勢い余って滑っていってしまう── 先に説明した高く投げたボールがヨレていくのと同じことです)。ちなみに高度3000mで重力ゼロになるのでその付近でのジャンプは自殺行為です(アプリ内でキャラは絶対死にませんけども)。高度2500mを越えたあたりからジャンプすると戻れない場合が多くなるので高高度は要注意です。手摺りの摩擦を若干大きめに設定してるので端っこに寄って手摺りに押しつけると擬似的に手摺りにつかまってる事になりいくらか安全です。

ここまでは地面を歩きまわるキャラクターでの話ですが、もし空中に速度ゼロで浮いた状態からはじめたらどんな感じになるか見てみたくて宇宙船タイプのアバターも用意してみました。3DモデルアセットはNASAが無償で提供している月着陸船ですが、今年はアポロ着陸50周年なのに日本ではイマイチ盛り上りがなくて寂しいワタクシです…。それはともかくメニューで LM のキャラクターを選択すると、高度3000mで速度ベクトルゼロ、角速度ゼロで浮かんだ状態からスタートします。LM は他のキャラより操作が難しいのですがそのかわり速度・回転の6軸を自由に操れるようになっています(実装の都合で下降スラスターだけ無いですが)。

クリックでビデオを再生

コントロールは難しいですがこれが結構面白くてハマります(昔アタリの Luna Lander にハマったオッサンにお勧め)。回転はできるだけきっちり止めて、ベロシティの変更はメインスラスターを積極的に使うのがコツです。計器類が無いのでGキーによるベロシティ表示だけが頼りです。ベロシティの方向にメインノズルが向くように姿勢をすばやく安定させ、スペースキーでメインスラスターをフカしてベロシティの上下成分をゼロ近くまで減少させた後に、残った横の成分はカーソルキーのサブスラスターで減少させる。こんな感じで慣れるとそこそこ自由に動きまわれるようになります。

空中からスタートして狙ったポイントに軟着陸できるか何度もトライしたのですが、これがかなり難しい！ 実際にアプリで体験してみてもらうとわかるのですが周囲の巨大なシリンダーの自転に惑わされて自分がどこへ向おうとしてるのかすぐに見失ってしまいます。アプリの開発初期は「ん？？ベロシティーが実際の移動方向とズレてるような…？バグ？？」と何度もデバッグデータを確認してみる事もありました。もし月着陸船をプレイしていて「アレ？このベロシティ表示バグってない？？」って思ったアナタ、それ錯覚です。パイロットに良く知られた、飛行中に自機の姿勢を錯覚してしまう“バーティゴ”という現象がありますが、宇宙港からスペースコロニーに侵入して着陸しようとする宇宙船のパイロットは常時バーティゴ状態と言って良いかもしれません。

さいわいオニールタイプのスペースコロニーには太陽光を取り込む大きな窓があるので、そこから見える宇宙の星々を基準にするように心掛けると錯覚を追い払うことができます。しかし宇宙を基準にした状態から地面を基準にした状態へ遷移する途中が惑わされやすくすぐに機位を見失ってしまい気がついた時には地面にハードランディングしてしまっていることはしょっちゅうです。自分で何度もプレイしてみて、スペースコロニーってなんだか超特大のびっくりハウスのようなもんだなーと思いましたね。

シミュレーションの実装について

シミュレーションについては運動を記述する計算式を事前に用意して組みこむようなことはやらずに、愚直にコロニーの設定サイズどおりに Unity のコライダーを並べて、挙動は組み込みの物理エンジンにまかせてあります。先入観なしでスペースコロニー内での物体の運動を見てみたかったのと、ぶっちゃけ計算式をこねくりまわすのが面倒くさかったからですが、実際にやってみると Unity の物理エンジンで想定してないような極端でトリッキーなパターンを使うことが多く挙動を安定させたり結果を検証する手間がだいぶかかってしまったため、こんな面倒なら最初から計算式を導出して isKinematic = true で実装するほうがマシだったかも…と思う事が何度もありました。

まず世界が巨大な円筒構造ですから一般的なシナリー用の Terrain は使えず、巨大メッシュを配置してコロニーワールドを構築しなければなりません。アセットストアとかフリーモデルで適当なコロニーの3Dデータが無いか探してみたのですが見つからなかったのでエレベーター他いくつかの小物含め自分で Blender でモデリングしました。

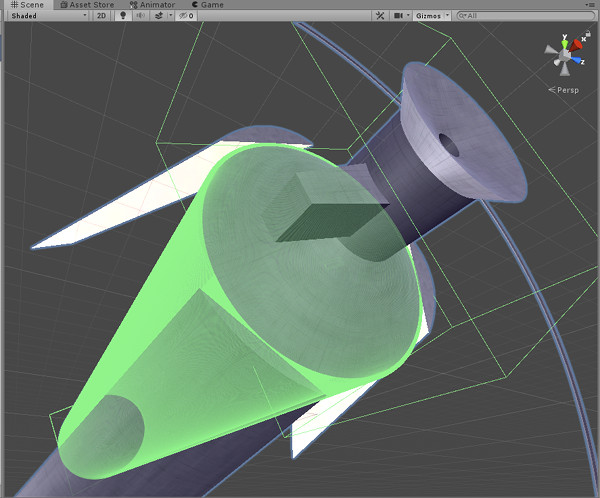
Unity の組み込みコライダーには中空のシリンダーは無いので、1024枚の板コライダーを円筒形に配置し円筒の両端はスクリプトで宇宙港まわりの特殊な形状判定をする箱コライダーで蓋をしてあります。最初は256枚のコライダーを使っていたのですがその程度だと歩いているだけでガタガタしているのがバレてしまう上に、板を接続している凹み部分でちょいちょい物理挙動が暴れてしまうため調整して1024枚になっております。コロニーを歩き回るとき地面…すなわちコロニーの壁の巨大ポリゴンに極めてスレスレに近づいてレンダリングしている状況になるため、コロニーのメッシュデータもコライダーとぴったりフィットしている必要があり(でないと歩いてるうちに壁をつきぬけたり不自然に浮いたりしてしまう)、したがってポリゴンモデルも1024枚の板ポリ分割になっているわけで、これもアプリが重くなる要因の一つとなっております。ちなみにメッシュとコライダーが一致してるならメッシュコライダーが使えるかというと、こういう物理エンジンのお約束ですがメッシュコライダーは凸形状(convex)でないと使えないか使えてもクソ遅いとか色々制限があったりするので要注意です。

余談ですが Unity5 以降は rigidbody の物理エンジンを利用する場合メッシュコライダは凸(convex == true)しか動作しなくなっています。おそらく汎用の non-convex メッシュコライダーはパフォーマンスの問題が大きすぎてサポートしきれない──と判断したように思われます。

1024枚ものコライダーすべてに動的に物理演算する Rigidbody をアタッチすると処理がとんでもなく重くなり現実的なプレイが不可能ですので、コロニー地面を構成する細っそながーい板はスタティックな箱コライダーです。ここで問題になるのが dynamic rigidbody コライダーと static コライダーが衝突する際の Unity 物理エンジンの挙動で、この場合双方の相対速度は無視されます。まあ当然といえば当然で別に Unity の実装が悪いとかいう話ではないのですが、この仕様により動的な rigidbody で動かされているキャラクターやボールはその rigidbody が保持する速度ベクトルでもって速度ゼロの地面にぶちあたっている状況になります。普通のゲームアプリならばキャラクターが走ったりしてる見た目の移動速度ベクトルそのままで移動しない地面にぶつかる状態なので別に問題はないわけですが、このシリンダーシムアプリの場合は前述のとおり地面もキャラもグローバル空間に対し600km/hオーバーで移動してるはずなのにキャラやボールは停止した地面に猛スピードでブチあたる状態になってしまうわけです。

もうすこし詳しい話をします。Unity の物理演算をいろいろ試してみたところ、このような状況でもキャラが地面に接触するときのトルクや作用反作用による運動量の変化などはおおむね正しく計算されます。しかし摩擦の計算において相対速度が無視されるため、ごくわずかの摩擦値(物理マテリアルfrictionプロパティ)を設定するだけでも接触した一瞬でものすごい減速と角運動量変化が発生してとんでもない方向に吹っ飛ばされてしまう挙動になります。なのでこのシムの地面の摩擦はゼロに設定しています。そのままだと地面がスケートリンクのようにツルツルになってしまうため、キャラと地面の間の摩擦はスクリプトで計算して減速がかかるように rigidbody の値に修正をかけています。また姿勢についても物理エンジンの計算そのままだとフラついたり時に荒ぶったりするので、安定して立つように rigidbody に補正をいれています。地面からキャラが離れるとそれらのスクリプトによる補正はすべて OFF になり Unity の物理エンジンのみで動作している状態になります。

このように Unity3D が想定するような、一定重力が下向きにあって固定した地面の上でキャラやオブジェクトが動きまわるような世界とはだいぶかけはなれた世界なので、3D表示でも色々と予想外の問題にブチあたって面倒な思いをしました。最初は安直に必要なメッシュモデル用意して Unity の組み込みシェーダーを適当にチョイスさえすれば、やっつけ感あってもそれなりの見栄えにできるだろうとタカをくくっていたのですが、Fog は平面世界を基準にした実装なので愚直に使おうとすると視野の変化につれてFogの境界が妙なところを移動してしまう(なのでシリンダーモデルの両端と本体の外側内側で別々のシェーダーをわりあてて個別にカスタムシェーダーを書いて対応)、各種エフェクトのシェーダーは Terrain で使う前提だったりY軸がグローバル空間の上固定になっていたりして、結局諸々のシェーダーを自前で書くハメになってしまいました。草シェーダーはだいたいどれも Terrain 前提になっているので、自前でテッセレーションを利用したええ感じのグラスシェーダーを書いたのですが、そもそも WebGL がテッセレーション対応してなかったのが判明、泣く泣くバーテックスシェーダーで上端ユラユラっていうショボいバージョンで書き直しました。まあこれは単なる私の事前調査不足ですが…。

ちなみに草はGPUインスタンシング(要WebGL2.0)を利用していますが、WebGLで大量のGPUインスタンシング使うと初回表示にものごっつう時間かかります──なので起動時に草を全部表示してからメニュー選択に移動する実装になってます(ローディング後に “Generating Objects…” とか言うてるのは誤魔化しで実際はインスタンシングしてる)

本当は河とか湖とか雲とか、あるいはスピード出てきたときにカッ飛んでる感を演出するための空中を舞うパーティクルとかを実装したかったんですけど、どれも有り物のシェーダーアセットは固定したグローバル空間でY軸上向きの世界で運用することを前提にしているため、単純に組みこむと地面に立っていても色んなものが時速600kmで流れ去りながら刻々と傾いていくような状態となり──なぜならグローバル空間ではシリンダーは自転していくので──結局あらゆるものを自作調達するハメになりそうだったのでやめました。そこまで苦労しても別にお金にもならんし…。

というわけで、もしこの記事をみてUnityで“スペースコロニー・シミュレーター”のゲームを実装してみようと考えてる方がおられましたら私のように物理エンジンをアテにして楽しようとするのはやめて、自キャラはグローバル空間の中心に固定しシナリーを構成する色々な物体は事前に導出した計算式を用意してスクリプトで transform を直に制御する方針(PCフライトシムの標準的な実装法とかなり近かったりしますが)でやったほうが、たぶん応用が効いて面倒は少なくなります。…たぶんね。…保証はしませんけど。

頑張ってエレベーターに乗って大宇宙港から外にでると宇宙船でのコロニー一周ツアーを見れます。